2019全国高中数学联赛加试T4引理证明

发表于

引理: 若一简单连通简单图$G(V, E)$中有$\vert E\vert$条边, 则该图中有$\lfloor \frac{E}{2} \rfloor$个两两无公共边的共点边对(下文称为"角"). [^1]

对$\vert V\vert$进行数学归纳(标答是对$\vert E\vert$)

$\vert V\vert=1$时显然成立

对于任意正整数$k$, 若$\vert V\vert<k$时结论成立, 下证$\vert V \vert=k$时结论成立

开始之前, 我们先分析一种简单的情况

对于任意点$V_0$, 若$degree(V_0)$为偶数

那么将$V_0$及与$V_0$相连的边两两去掉并计数, 剩下的图$G’(V’, E’)$满足$\vert V\vert<k$, 由归纳假设, 结论"成立"(为什么有引号)

这个反例还是挺容易构造的

如图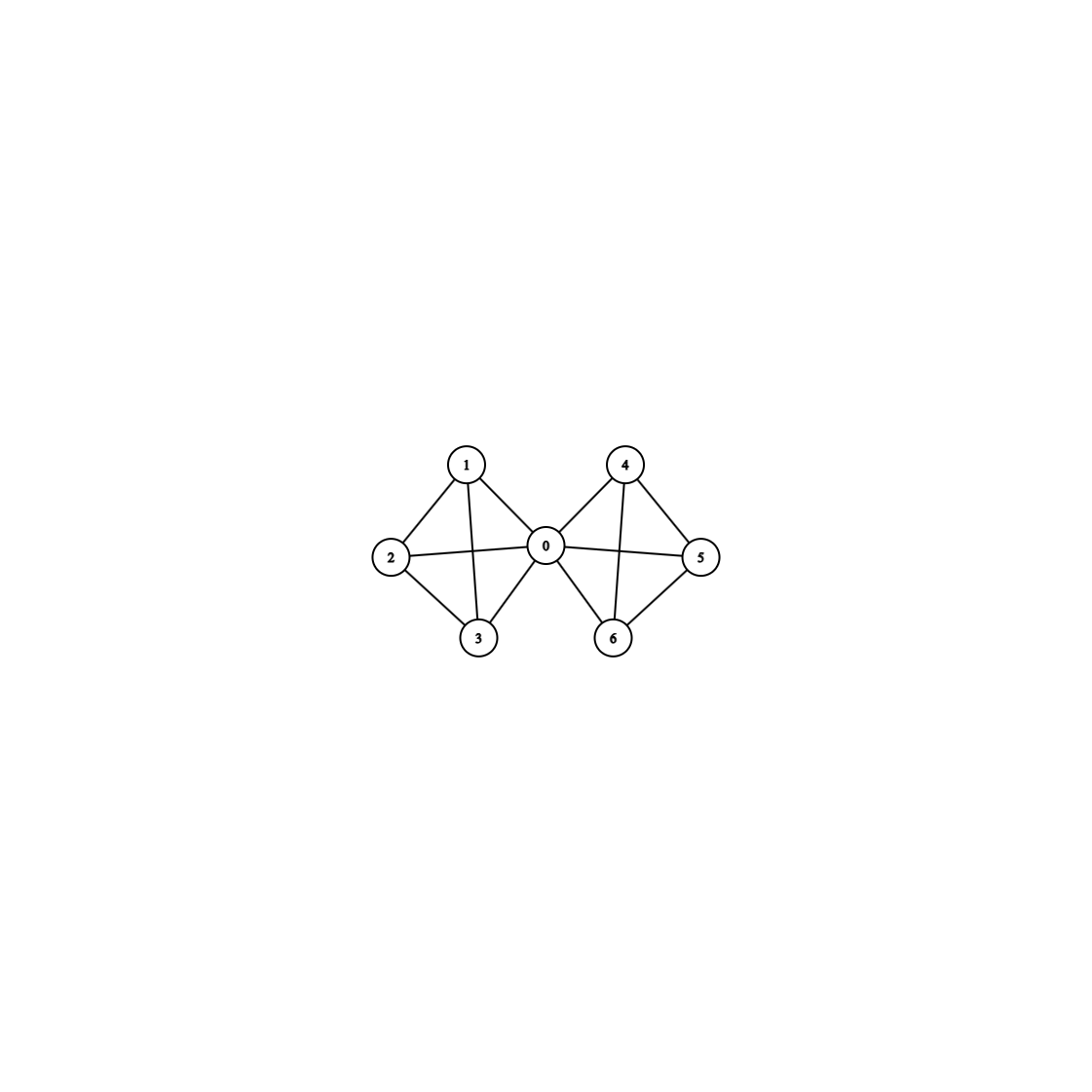graph1.png

$degree(V_0)$为偶数, 但显然我们不能这么做(想一想为什么)

因为剩下的$G’$不是一个连通图, 更要命的是$G’$的连通分量集中还有大于1个有奇数条边的连通分量

如图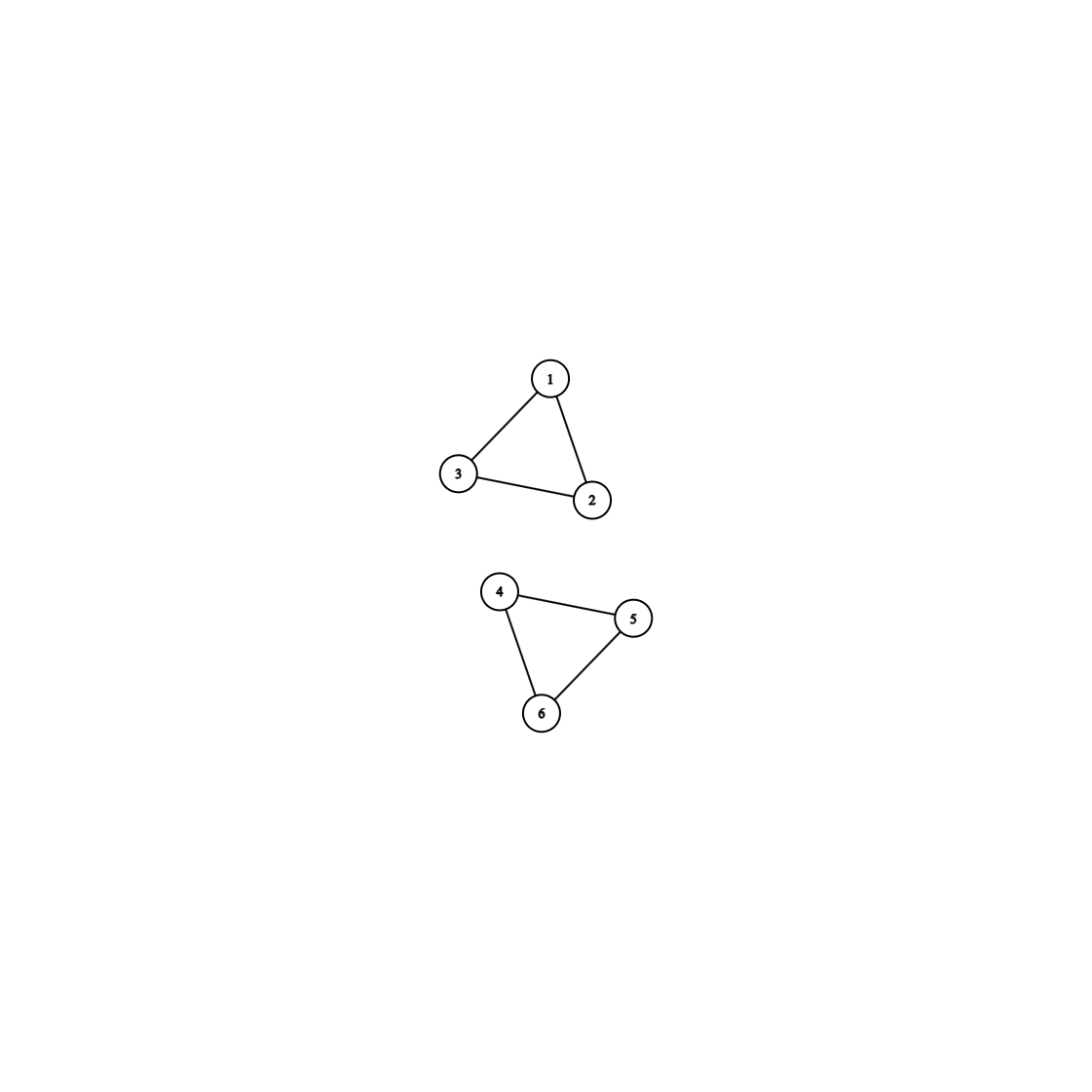graph2.png显然不成立

这种情况下再去"限制$G’$的连通分量集中有小于1个有奇数条边的连通分量"已经没有多大用处了

这种做法似乎走到了尽头…

除非…

$G$中没有割点!

没错, 没有割点就不会出现去掉一个点后剩下的图不连通(这是割点的定义! 同时, 我们由上面的推导中可以发现可作限制"剩下的$G’$是一个连通图", 进而联想到割点)的情况

这时再进行如上操作便合情合理, 即"存在$V_0$使$degree(V_0)$为偶数且$G$为点双连通分量时"结论成立

若$G$中没有度数为偶数的点呢?

这个好办, 你把任意一个"角"去掉不就有了吗? (这样就可以化归为上面或下面情况中的一种啦) [^2]

接下来考虑剩下的情况, 即"$G$中存在割点"的情况

如图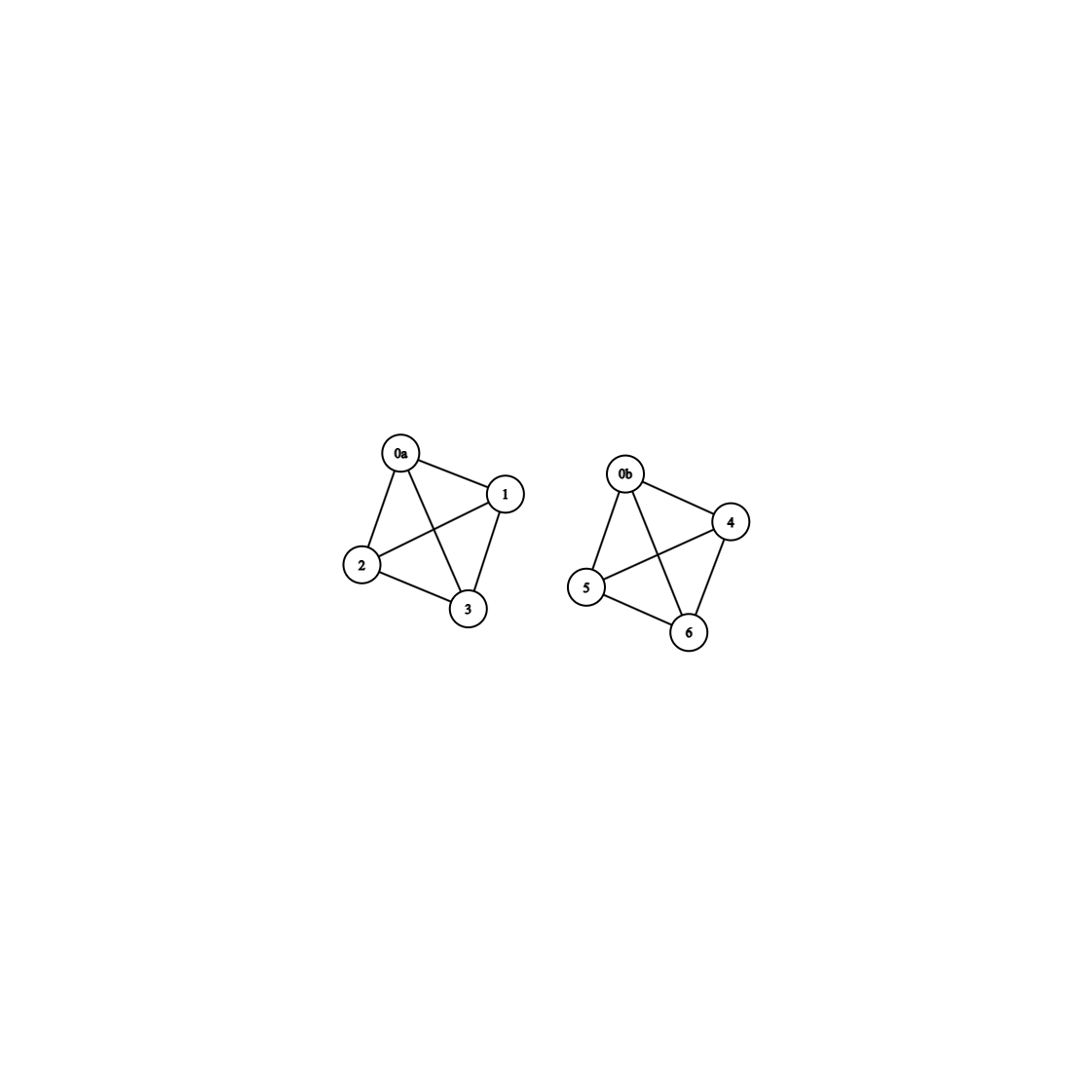graph3.png

我们去掉割点$V_0$后, 不妨设$G$被分为了$m$个连通分量$G_1(V_1, E_1), G_2(V_2, E_2), \dots , G_m(V_m, E_m)$, 设$V_0$与这些连通分量相连的边集分别为$E_{01}, E_{02}, \dots E_{0m}$

考虑$G_1’(V_1\cup V_0, E_1\cup E_{01}), G_2’(V_2\cup V_0, E_2\cup E_{02}), \dots , G_m’(V_m\cup V_0, E_m\cup E_{0m})$, 若$G_1’, G_2’, \dots , G_m’$中有$n$个含有奇数条边的图, 设为$G_{j1}, G_{j2}, \dots , G_{jn}$取n条边$E_1\in G_{j1}, E_2\in G_{j2}, \dots , E_n\in G_{jn}$可配成$\lfloor\frac{n}{2}\rfloor$个"角"(这时有人要问, 若$n$为奇数那又怎么办呢? 不是会剩下一条边无法配对吗? $n$为奇数说明原图$G$中有奇数条边, 本来就会剩下一条边, 又何必担心呢? ), 将这$n$条边全部去掉后$G_1’, G_2’, \dots , G_m’$均含有偶数条边, 且顶点数均小于$k$, 结论成立

综上所述, 得证

$Q.E.D.$

[^1]: 为什么只有引理? 因为后面我也不会了. 这个引理也是看标答才知道的…

[^2]: 其实有割点的情况应该放在前面写的, 这样就不会出现前面引用后面结论破坏连贯性的情况了, 但是为了体现思考过程, 避免看完以后出现"看懂了, 想不到"的情况, 姑且这么写吧.

本来计划2023-06-16 19:18:39开写的, 但实际上咕到了2023-06-23 22:59:56才写完…